IDENTIDADES TRIGONOMETRICAS

Identidades del ángulo múltiple

Si T_n es el n-simo Polinomio de Chebyshev entonces

$\cos(nx)=T_n(\cos(x)).$

$\cos(nx)+i\sin(nx)=(\cos(x)+i\sin(x))^n$

Identidades del ángulo doble, triple y medio

Pueden obtenerse remplazándolo y por x (o sea $\sin(x+x)=\sin(2x)$ ) en las identidades anteriores, y usando el teorema de Pitágoras para los dos últimos (a veces es útil expresar la identidad en términos de seno, o de coseno solamente), o bien aplicando la Fórmula de De Moivre cuando $n = 2$ .

Fórmula del ángulo doble
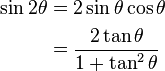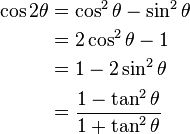$\begin{align} \sin 2\theta &= 2 \sin \theta \cos \theta \ \\ &= \frac{2 \tan \theta} {1 + \tan^2 \theta} \end{align}$	$\begin{align} \cos 2\theta &= \cos^2 \theta - \sin^2 \theta \\ &= 2 \cos^2 \theta - 1 \\ &= 1 - 2 \sin^2 \theta \\ &= \frac{1 - \tan^2 \theta} {1 + \tan^2 \theta} \end{align}$	$\tan 2\theta = \frac{2 \tan \theta} {1 - \tan^2 \theta}\,$	$\cot 2\theta = \frac{\cot \theta - \tan \theta}{2}\,$
Fórmula del ángulo triple
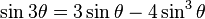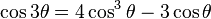$\sin 3\theta = 3 \sin \theta- 4 \sin^3\theta \,$	$\cos 3\theta = 4 \cos^3\theta - 3 \cos \theta \,$	$\tan 3\theta = \frac{3 \tan\theta - \tan^3\theta}{1 - 3 \tan^2\theta}$
Fórmula del ángulo medio
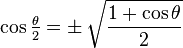$\sin \tfrac{\theta}{2} = \pm\, \sqrt{\frac{1 - \cos \theta}{2}}$	$\cos \tfrac{\theta}{2} = \pm\, \sqrt{\frac{1 + \cos\theta}{2}}$	$\begin{align} \tan \tfrac{\theta}{2} &= \csc \theta - \cot \theta \\ &= \pm\, \sqrt{1 - \cos \theta \over 1 + \cos \theta} \\ &= \frac{\sin \theta}{1 + \cos \theta} \end{align}$	$\cot \tfrac{\theta}{2} = \csc \theta + \cot \theta$

Producto infinito de Euler

$\cos\left({\theta \over 2}\right) \cdot \cos\left({\theta \over 4}\right) \cdot \cos\left({\theta \over 8}\right)\cdots = \prod_{n=1}^\infty \cos\left({\theta \over 2^n}\right) = {\sin(\theta)\over \theta}.$

Identidades para la reducción de exponentes

Resuelve las identidades tercera y cuarta del ángulo doble para cos²(x) y sin²(x).

Seno	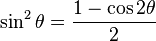$\sin^2\theta = \frac{1 - \cos 2\theta}{2}$	$\sin^3\theta = \frac{3 \sin\theta - \sin 3\theta}{4}$
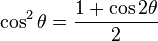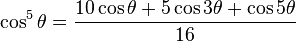Coseno	$\cos^2\theta = \frac{1 + \cos 2\theta}{2}$	$\cos^3\theta = \frac{3 \cos\theta + \cos 3\theta}{4}$	$\cos^5\theta = \frac{10 \cos\theta + 5 \cos 3\theta + \cos 5\theta}{16}$
Otros	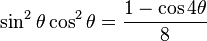$\sin^2\theta \cos^2\theta = \frac{1 - \cos 4\theta}{8}$	$\sin^3\theta \cos^3\theta = \frac{\sin^3 2\theta}{8}$